
Constitutive Equations of Piezoelectricity
In the linear theory of the piezoelectric effect, a description of the small-signal behavior was developed (for further information see * 1 * 2). This theory does not include non-linear effects or the hysteresis of piezoelectric materials, which is particularly significant in the large-signal range. However, the linear equations are extremely valuable as they provide a good understanding of the physics of piezo actuators. Effective large-signal parameters must be applied to actuators. The behavior of piezo actuators (inverse effect) can be described mathematically in matrix notation as follows:
Sj = dij Ei
Sj is the load (in m per m), dij is the piezoelectric charge coefficient (m/V) Ei is the electric field (in V/m). Typical values for the maximum load are 0.2% at an electric field of 2 kV / mm. The indices i and j indicate the direction. For stack actuators, the direction of the applied field and that of the strain is the stack axis, which is usually indicated by the index 3. Thus, the relevant material parameters are the d33 coefficient and the strain S3 is equal to d33 x E3. In the further discussion, the matrix notation is simplified using scalar equations.
It is obvious that piezoelectric actuators involve two phenomena: the mechanics of a solid body and the dielectric behavior of a capacitor. In the first instance, both aspects are described decoupled. This means that either the electrical state (e.g. terminals of a piezo stack actuator are short-circuited) or the mechanical state is kept constant (e.g. the actuator is ideally fixed and the length is invariable). The mechanical constitutive equation that applies to piezo materials (also known as Hooke's law) is:
S = s T
In words, this equation says: elongation = compliance × load pressure This formula can be applied to the deformation of the actuator body:
x = s A / l F
In other words, this equation says: Displacement x is equal to compliance times base area divided by height and force.

Piezoelectric materials have electrical properties. We must use the equation of state for common dielectrics:
D = eps E
In words: This equation is: Charge density = dielectric constant × electric field. This formula can be converted for a piezoelectric actuator body:
Q = eps A / l = C U
In words, this equation determines: Charge = dielectric constant x base area divided by height and Electric field equal to the product of the electric capacitance and the voltage. For piezoelectric materials, these two constitutive equations must be applied to a coupled equation, which is written as follows:
S = S T + D E
D = d + e T E
The parameters of a piezo component, which are the mechanical stiffness k, force F, charge Q, can be calculated from the above equations. The observable variables at the terminals of the actuator are the electrical voltage U, length, displacement, force and electrical current. The electric charge Q, which is fundamentally important for the piezo effect, can only be observed through the time integral of the electric current:
Q = Integral I dt
Consequently, the electromechanical coupling mechanism manifests itself in a linear relationship between the rate of change in length and the electrical current.he elastic behavior of the body (contraction in response to compressive forces) is superimposed by the piezoelectric deformation effect (internal electrical forces cause elongation). Also, the electric charge of the piezo, represented by a capacitor, is the sum of two terms: 1) charging of a capacitor C by an applied electric voltage U and 2) a charge caused by the deformation of the piezoelectric crystals by the applied force. The next figure illustrates the coupling of electrical and mechanical phenomena through the piezoelectric effect.
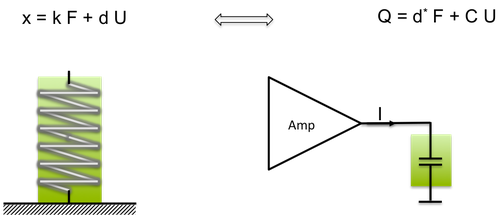
If a problem requires a three-dimensional analysis, the piezoelectric coupling elements can be formulated in a matrix representation d.
* 1 Cady, WG, Piezoelektrizität, McGraw Hill, New York (1946)
* 2 Cook & H Jaffe, piezoelektrische Keramiken, Academic Press, London (1971)