Piezo Stack Under Spring Mass Load
All real mechanical system has mass and spring characteristics. In a dynamic analysis the inertia forces must be considered with a mass dependent term. The simplest case is a stack itself in highly dynamic operation. In the next differential equation of motion the Newton’s law are expressed in a lumped parameter model:
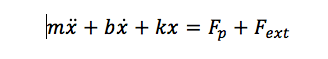
Fp is the piezoelectric force controlled by the voltage, x is the displacement, m the effective inertial mass of the piezo, and k is a term for damping.
This equation represents a damped spring-mass system, which will perform damped oscillation when excited by a voltage step function. The following data are exemplarily presented for a Piezotechnik PB5.8 stack:
· fres 76 kHz
· meff 3,4 grams
· stiffness k 6 000 N/m equivalent to a effective Young’s modulus of 44 GPa
· damping parameter b 150 Ns/m
It is well known that this dynamic system have a resonance effect and will overshoot and ring when excited with a voltage step function. The actuator has a large initial acceleration a0
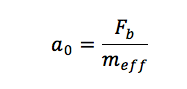
In the chosen example the initial acceleration of the stack a0 is 250 000 m/s2 or 25 500 g. In a practical case there will be a load mass and resonance frequency would be reduced of course.
Rise time for spring-mass system is usually approximated by tr = 1/3fres. In the given example t = 5 ms. Please notice, that for faster dynamic operation a dynamic overshoot reaction occurs. An overshoot over the maximum static displacement cause internal stress in the ceramics in tensile direction. As ceramics is sensitive to tensile stress compensation by pre-stress is required to avoid cracking and failure of the piezo. Those pre-stress mechanism cause mass effort and will reduce reaction speed of the actuator.
These physics principles has to be taken in consideration when designing a piezo stack actuation mechanism for strong, fast and precise systems.
Performance made of Passion.
Piezotechnics by
Piezotechnics GmbH
Germany
