Piezo Actuators - Constitutive Equations
A linear theory of piezoelectric phenomena effect was developed which describes small signal behaviour (for further reading see *1 *2 ). This theory does not comprise nonlinear effect and hysteresis. But, the linear equations provide a good understanding of the physics of piezo actuators. For piezo actuators effective large signal parameters have to be applied.
Piezo actuation (inverse effect) can be described mathematically in matrix notation as:
Sj = dij Ei
Sj is the strain (in m per m), dij is the piezoelectric charge coefficient (m/V) Ei is the electric field (in V/m). Typical values for maximum strain is 2000 micro strain or 0.2% and electric field is 2 kV/mm. The subscripts i and j indicate the direction. For stack actuators the direction of applied field as well as strain is the stack axis, which are indicated by the subscript 3. Thus the relevant material parameter is the d33 coefficient and strain S3 is equal d33 x E3. In the further discussion the matrix notation is simplified to scalar equations.
Strain of Piezo Actuators
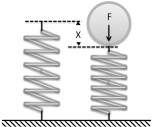
In words, this equation states: displacement x = compliance × base area / height x force.
Piezoelectric materials are concerned with electrical properties too. We must also consider the constitutive equation for common dielectrics:
D = eps E
In words, this equation states: Charge Density = Permittivity × Electric Field.
This formula can be transformed to an actuator body:
Q = eps A/l = C U
In words, this equation states: Charge = Permittivity x base Area / height x Electric Field equal electrical capacity x Voltage.
Coupling of Mechanical and Electrical Behavior
Piezo materials combine these two constitutive equations into one coupled equation, written as:
S = s T + d E
D = d T + e E
The parameter of a piezo component: mechanical stiffness k, force F, charge Q can be calculated from these equations. The observable quantities at the terminals of the actuator are electrical voltage U, length, displacement, force and electrical current. The electrical charge Q, which is fundamental important for the piezo effect, is observable by the time integral of electrical current.
Q = Integral I dt
In consequence, the electro-mechanical coupling mechanism results in a linear relation between speed of displacement and electrical current.
The coupling of electrical and mechanical phenomena by the piezo effect is illustrated in the next figure. The elastic behaviour of the body (contraction as a reaction of compressive forces) is superimposed by the piezoelectric strain effect (internal electric forces cause strain). Also, the electrical charge of the piezo, which is represented by a capacitor, is the sum of two terms: 1) charging a capacitor C by an applied electrical voltage U and 2) a charge, which result of the deformation of piezoelectric crystals by the applied force. The next figure summarizes the coupling of mechanical and electrical phenomena:
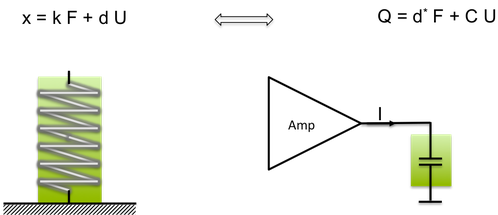
If a problem needs a three-dimensional analysis the piezoelectric coupling terms can be formulated in a comprehensive matrix representation d. In this frame the description of a piezoelectric material requires knowledge about the material’s mechanical properties (compliance or stiffness), its electrical properties (permittivity), and its piezoelectric coupling properties.
Strain-Charge Relation
S = sE T + dT E
D = dT + epsT E
Strain Voltage Relation
S = sD T + gt D
E = -g T + eT-1 D
Stress Voltage Relation
T = cD S –qt D
E = -q S + epsT-1 D
Stress-Charge Relation
T = cE S –et E
D = -q S + epsS -1 D
Meaning
eps dielectric constant
T vector 6 x 1 [N/m2] stress components (e.g. σ1)
S vector 6 x 1 [m/m] strain components (e.g. S3)
E vector 3 x 1 [V/m] electric field components
D vector 3 x 1 [C/m2] electric charge density displacement components
s matrix 6 x 6 [m2/N] compliance coefficients
c matrix 6 x 6 [N/m2] stiffness coefficients
e matrix 3 x 3 [F/m] electric permittivity
d matrix 3 x 6 [N/m2] coefficients for Strain-Charge form
e matrix 3 x 6 [C/m2] coefficients for Stress-Charge form
g matrix 3 x 6 [m2 /C] coefficients for Strain-Voltage form
q matrix 3 x 6 [C/N] coefficients for Stress-Voltage form
*1 Cady, W G, Piezoelectricity, McGraw Hill, New York (1946)
*2 Cook & H Jaffe , Piezoelectric Ceramics, Academic Press, London (1971)
Performance made of Passion.
Piezotechnics by
Piezotechnics GmbH
Germany
